Feld­be­rech­nung mit der Ran­d­ele­ment­me­tho­de im Win­ter­se­mes­ter 2022/2023

Inhaltsbeschreibung

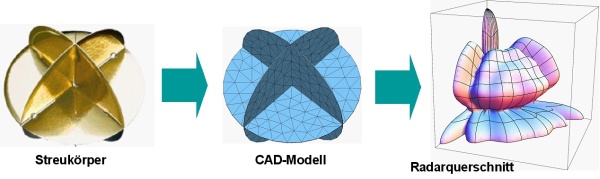
Entwicklung, Design und Optimierung technischer Bauteile oder Geräte erfordern eine adäquate Beschreibung der darin ablaufenden physikalischen Prozesse in Form mathematischer Modelle, die aufgrund ihrer hohen Komplexität im Allgemeinen nur unter Zuhilfenahme numerischer Feldberechnungsverfahren analysiert werden können. Ein Vertreter davon ist die Randelementmethode, die bevorzugt in der Antennentechnik zur Lösung von Abstrahlungsproblemen sowie in der Radartechnik zur Untersuchung von Streuobjekten eingesetzt wird, woraus wichtige Kenngrößen wie beispielsweise die Richtcharakteristik von Antennen oder der Rückstreuquerschnitt von Radarzielen ableitbar sind.

Ziel der Vorlesung ist die Vermittlung des theoretischen Basiswissens über die Randelementmethode unter Berücksichtigung anwendungsbezogener Aspekte, wobei das Hauptaugenmerk auf den Einsatz in der Ingenieurspraxis gerichtet ist. Im Mittelpunkt stehen die als Integralgleichungsmethode bezeichnete Überführung elektromagnetischer Randwertprobleme in dazu äquivalente Integralgleichungen und deren Diskretisierung mit Hilfe der Momentenmethode, die in ihrer Gesamtheit die Randelementmethode bilden. Besonderer Wert wird dabei auf die mathematische Modellierung von Antennen-, Eigenwert- und Streuproblemen sowie die Extraktion charakteristischer Zielgrößen aus der Feldlösung gelegt, um so den wichtigen Bezug zur Rechenpraxis herzustellen. Typisch für dieses Diskretisierungsverfahren ist das Auftreten singulärer Integrale, die gewöhnlich nicht analytisch lösbar sind. Um diese einer numerischen Auswertung unter Verwendung herkömmlicher Kubaturverfahren zugänglich machen zu können, sind spezielle Regularisierungstechniken zwingend erforderlich, die vorgestellt und in Hinblick auf ihre Leistungsfähigkeit miteinander verglichen werden. Strategien zur Lösung des diskreten Problems sowie Möglichkeiten zur Beschleunigung des Lösungsprozesses, die aufgrund dicht besetzter Systemmatrizen unumgänglich ist, werden ebenfalls besprochen.

Die Vorlesung wird von einer programmierpraktischen Übung begleitet, in welcher die in der Vorlesung präsentierten Algorithmen auf einem Computer umgesetzt und anhand einfacher Praxisbeispiele erprobt werden sollen.

Themengebiete

1. Einführung
   • Motivation
   • Mathematische Grundlagen
2. Integralgleichungsmethode
   • Darstellungsformeln für elektromagnetische Felder
   • Oberflächenintegralgleichungen
3. Mathematische Modellbildung
   • Formulierung von Antennen-, Streu- und Eigenwertproblemen
   • Anregungsformen
   • Berechnung von Rückstreuquerschnitten und Antennenparametern
4. Diskretisierung mittels Momentenmethode
   • Prinzip von Projektionsverfahren
   • Basisfunktionen
5. Berechnung der Matrixbeiträge
   • Numerische Integration
   • Behandlung singulärer Integrale
6. Aspekte bei der Lösung des diskreten Modellproblems
   • Lösungsstrategien
   • Matrixkompressionsverfahren

Literaturempfehlung

• S. Sauter, C. Schwab: "Randelementmethoden", Teubner-Verlag, Lehrbuch
• A. F. Peterson et. al.: "Computational Methods for Electromagnetics", IEEE-Press, Lehrbuch

Hinweise:

• Die Veranstaltung findet nur bei hinreichender Teilnehmerzahl statt.
• Die Festlegung der Termine für die Vorlesung und Übung erfolgt in Absprache mit den Teilnehmern ca. eine Woche vor Beginn der Vorlesungszeit.